[コンプリート！] p xor q xor r truth table 237840-P xor q xor r truth table

I made this app just for you quickly generate truth tables from any boolean logic statement it also includes an interactive tutor that teaches you how to solve truth tables stepbystep!Strugging with truth tables?Truth Table Generator This page contains a JavaScript program which will generate a truth table given a wellformed formula of truthfunctional logic You can enter multiple formulas separated by commas to include more than one formula in a single table (eg to test for entailment)

Gate Cse 14 Set 3 Question 55 Gate Overflow

P xor q xor r truth table

P xor q xor r truth table-Truth table p XOR q XOR r XOR s Extended Keyboard;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Truth table The truth table of p X O R q {\displaystyle p\,\mathrm {XOR} \,q} (also written as p ⊕ q {\displaystyle p\oplus q} , p ⊻ q {\displaystyle p\veebar q} , 1 or p ≠ q {\displaystyle p\neq q} ) is as follows 2The XOR function can accommodate any number of inputs Whether a physical XORgate exists with more than 2inputs is one thing, as is whether we defined XOR purely in terms of exclusive disjunction hence limiting the XORgate to 2inputsThe truth table for XOR is p q XOR 0 0 0 0 1 1 1 0 1 1 1 0 We can construct an expression for XOR in terms of AND, OR, and NOT, using the following reasoning The second row tells us that p XOR q is TRUE when p is FALSE and q is TRUE In other words, p XOR q is TRUE if NOT p AND q is TRUE The third row tells us that p XOR q is TRUE when

P XOR q has truth table (XOR = exclusive OR) p q (p XOR q) 0 0 0 0 1 1 1 0 1 1 1 0 ie the result is true when only one of p or q is true The Exclusive OR operator in C is ^ Your logic statement can be broken down using a truth tableExample 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalentTruth tables list the output of a particular digital logic circuit for all the possible combinations of its inputs The truth table of an XOR gate is given below The above truth table's binary operation is known as exclusive OR operation It is represented as A ⊕ B The symbol of exclusive OR operation is represented by a plus ring surrounded by a circle ⊕

P q r (p V q) (q→r) etc until it gets to (((p∨q)∧((q→r)⊕(p∧r)))↔(r∧q))→(p∨r) t t t t t t t f t f t f t t t t f f t t f t t t t f t f t f f f t f t f f f f t i devised a way to deal with the XOR and implies operators, but I realized that it only works when the operators are inside the inner parentheses, not when theThis tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats For example, the propositional formula p ∧ q → ¬r could be written as p /\ q > ~r, as p and q => not r, or as p && q > !r The connectives ⊤ and ⊥ can be entered as T and FEach statement of a truth table is represented by p,q or r and also each statement in the truth table has their respective columns that list all the possible true values The output which we get is the result of the unary or binary operations executed on the input values Some of the examples of binary operations are AND, OR, NOR, XOR, XNOR, etc

Logic Part 1 Propositions And Truth Values Vigorouslyrigorous

Applied Propositional Logic Theory Simulation Code And Digital Circuit Design Mathematical Science Technologies

Informally, the truth table indicates associativity of XOR, or equivalently that {(p⊕q)⊕r=p⊕(q⊕r)} qualifies as a tautology, where "=" indicates the operation of logical equivalence By the completeness metatheorem (every tautology is a theorem) of really any system of classical propositional logic that you probably will encounterThis truthtable calculator for classical logic shows, well, truthtables for propositions of classical logic Featuring a purple munster and a duck, and optionally showing intermediate results, it is one of the better instances of its kindExclusive or or exclusive disjunction is a logical operation that outputs true only when inputs differ (one is true, the other is false) It is symbolized by the prefix operator J and by the infix operators XOR (/ ˌ ɛ k s ˈ ɔːr / or / ˈ z ɔːr /), EOR, EXOR, ⊻, ⩒, ⩛, ⊕, ↮, and ≢The negation of XOR is logical biconditional, which outputs true only when the two inputs are

Arxiv Org Pdf 1412 2287

Truth Tables Brilliant Math Science Wiki

A truth table has one column for each input variable (for example, P and Q), and one final column showing all of the possible results of the logical operation that the table represents (for example, P XOR Q) Each row of the truth table contains one possible configuration of the input variables (for instance, P=true Q=false), and the result of the operation for those valuesHappy Baby Pose yoga curve vs Woody Woodpeckerlike curve vs Doctor Sivanalike curve;You can do that and help support Ms Hearn Mat

Http Sc Sogang Ac Kr Download Pathstr Ndgjizu1iym0ocmjndkjizeyncmjmta0iymxmtyjizk3iym4mcmjmtaxiymxmdgjizewnsmjmtayiymznsmjmzmjizm1iym0osmjmti0iymxmjajizewmsmjmtawiymxmtajizewnsmjmzujizmziymznsmjntejizuziym1nymjndgjizuxiymxmjqjizewmcmjmta1iymxmdcjizexmg Filename D Math 18 Ch1 Part1 Logic And Proofs Pdf Gubun Board

Boolean Algebra Basic Laws Baeldung On Computer Science

Compute expertlevel answers using Wolfram's breakthrough algorithms, knowledgebase and AI technologyTwo propositions p and q are called logically equivalent if and only if vp = vq holds for all valuations v on Prop In other words, two propositions p and q are logically equivalent if and only if p 㲗 q is a tautology We write p ≡ q if and only if p and q are logically equivalent We have shown that (¬p ⋁q) ≡ (p q)7 Logical operators XOR • An exclusive or operation is true if one of the operands are true, but false if both are true • Symbol • Often called XOR • p q (p q) ¬(p q) • p q = "Today is Friday or today is my birthday, but not both" p q p q T T F T F T F T T F F F EECE2160

Exclusive Or Wikipedia

How To Input Xor Into A Truth Table Generator Quora

Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false) It is symbolized by the prefix operator J and by the infix operators XOR (/ ˌ ɛ k s ˈ ɔːr / or / ˈ z ɔːr /), EOR, EXOR, ⊻, ⩒, ⩛, ⊕, ↮, and ≢The negation of XOR is logical biconditional, which is true if and only if the two inputsEach statement of a truth table is represented by p,q or r and also each statement in the truth table has their respective columns that list all the possible true values The output which we get is the result of the unary or binary operationsTwo propositions p and q are called logically equivalent if and only if vp = vq holds for all valuations v on Prop In other words, two propositions p and q are logically equivalent if and only if p 㲗 q is a tautology We write p ≡ q if and only if p and q are logically equivalent We have shown that (¬p ⋁q) ≡ (p q)

Logic And Truth Tables Application Center

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

This is just the truth table for \(P \imp Q\text{,}\) but what matters here is that all the lines in the deduction rule have their own column in the truth table Remember that an argument is valid provided the conclusion must be true given that the premises are true The premises in this case are \(P \imp Q\) and \(P\text{}\)Truth tables list the output of a particular digital logic circuit for all the possible combinations of its inputs The truth table of an XOR gate is given below The above truth table's binary operation is known as exclusive OR operation It is represented as A ⊕ B The symbol of exclusive OR operation is represented by a plus ring surrounded by a circle ⊕Welcome to the interactive truth table app This app is used for creating empty truth tables for you to fill out Just enter a boolean expression below and it will break it apart into smaller subexpressions for you to solve in the truth table The app has two modes, immediate feedback and 'test' mode

S2 1

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Welcome to the interactive truth table app This app is used for creating empty truth tables for you to fill out Just enter a boolean expression below and it will break it apart into smaller subexpressions for you to solve in the truth table The app has two modes, immediate feedback and 'test' modeTruth Table Generator This tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats For example, the propositional formula p ∧ q → ¬r could be written as p /\ q > ~r, as p and q => not r, or as p && q > !rConstruct a truth table for each of these compound propo sitions a p q r b p q from CICT 106 at University of Batangas Study Resources without using a truth table, why (p ∨ q ∨ r) XOR (x 2 = 3) then x = x 1 e) if x < 2 then x = x 1 47 Find the bitwise OR, bitwise AND, and bitwise XOR of each of these pairs of bit strings

Webunit2

Practice Free Questions For Gate Ec Electronics And Communication Engineering Digital Circuits Nthexam

Have a question about usingI have an assignment where I need to demonstrate whether or not (p xor q xor r) is equivalent to (p⇔q⇔r) I need to do this without the use of truth tables, so I just wanted to know if there was some equivalency laws regarding exclusive or relating to biconditional which would make the solution to this problem a little more clearerIf the truth table for a NAND gate is examined or by applying De Morgan's Laws, it can be seen that if any of the inputs are 0, then the output will be 1To be an OR gate, however, the output must be 1 if any input is 1 Therefore, if the inputs are inverted, any high input will trigger a high output

Is The Associative Property Of Xor Provable Or Axiomatic Mathematics Stack Exchange

Question Video Evaluating The Output Of Multiple Xor Gates Using Truth Tables Nagwa

Click SHOW MORE to view the description of this Ms Hearn Mathematics video Need to sell back your textbooks?XOR PQ P XOR Q TT F TF T FT T FF F 312 IMPLIES The combining operation with the least intuitive technical meaning is "implies" Here is its truth table, with the lines labeled so we can refer to them later PQ P IMPLIES Q TT T (tt) TF F (tf) FT T (ft) FF T (ff) The truth table for implications can be summarized in words asTruth table p xor q xor r xor s Extended Keyboard;

Osa Topological All Optical Logic Gates Based On Two Dimensional Photonic Crystals

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Truth Table is used to perform logical operations in Maths These operations comprise boolean algebra or boolean functions These operations comprise boolean algebra or boolean functions It is basically used to check whether the propositional expression is true or false, as per the input valuesExample 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalentSimplify p xor q xor r xor s;

Q Tbn And9gctl2zcptshv3iyzy8meoqsjchgvcibdk4dy7nnneafmqmi2cwbv Usqp Cau

Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium

The truth table for XOR is shown below p q p XOR q T T F T F T F T T F F F It seems like we use "or" as exclusive sometimes and inclusive other times My colleagues and I were talking about this at the lunch table the other day One of my colleagues presented a simple example that illustrates this confusionRegardless of the truth of P (as long as P is not both true and false!), this is always false Construct a truth table for "if ( P if and only if Q) and (Q if and only if R), then (P if and only if R)" This will always be true, regardless of the truths of P, Q, and R This is another way of understanding that "if and only if" is transitiveWhether a physical XORgate exists with more than 2inputs is one thing, as is whether we defined XOR purely in terms of exclusive disjunction hence limiting the XORgate to 2inputs If you are dealing with XORgates in an academic capacity then you will come across XORgates with more than 2inputs

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

2

Welcome to the interactive truth table app This app is used for creating empty truth tables for you to fill out Just enter a boolean expression below and it will break it apart into smaller subexpressions for you to solve in the truth table The app has two modes, immediate feedback and 'test' modeThis is the first time I've heard of that website, so I'm not sure if it has a dedicated exclusiveor operator, but you could certainly synthesise it by excluding the conjunction explicitly code(p \/ q) /\ ~(p /\ q) /codeIn other words, (p orEach statement of a truth table is represented by p,q or r and also each statement in the truth table has their respective columns that list all the possible true values The output which we get is the result of the unary or binary operations executed on the input values Some of the examples of binary operations are AND, OR, NOR, XOR, XNOR, etc

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Dl Q1 Boolean Algebra Teaching Mathematics

Input interpretation Truth table Download Page POWERED BY THE WOLFRAM LANGUAGE Related Queries p xor q xor r xor s;Compute expertlevel answers using Wolfram's breakthrough algorithms, knowledgebase and AI technologyExclusive OR (XOR) Gate is Logical Gate which gives High Output signal when the no of High input signal is odd Symbol of Exclusive OR (XOR) Gate is given here Truth Table of XOR Gate is explained here Internal circuit design of XOR gate is described here Example of XOR Gate ICs given here

Ocw Mit Edu Courses Electrical Engineering And Computer Science 6 042j Mathematics For Computer Science Spring 15 Proofs Tp2 2 Truth Tables Video Truth Tables 3wdzxt5p8c Pdf

Complex Logical Forms Exercises 8 2 Number The Ope Chegg Com

P XOR q has truth table (XOR = exclusive OR) p q (p XOR q) 0 0 0 0 1 1 1 0 1 1 1 0 ie the result is true when only one of p or q is true The Exclusive OR operator in C is ^ Your logic statement can be broken down using a truth tableXOR PQ P XOR Q TT F TF T FT T FF F 312 IMPLIES The combining operation with the least intuitive technical meaning is "implies" Here is its truth table, with the lines labeled so we can refer to them later PQ P IMPLIES Q TT T (tt) TF F (tf) FT T (ft) FF T (ff) The truth table for implications can be summarized in words asExample 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalent

Solved 31 The Exclusive Disjunction Of Two Propositions Chegg Com

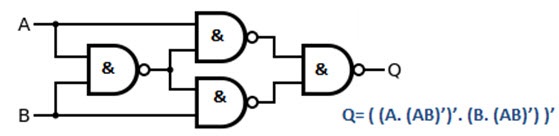
Exclusive Or Gate Xor Gate

This is the first time I've heard of that website, so I'm not sure if it has a dedicated exclusiveor operator, but you could certainly synthesise it by excluding the conjunction explicitly code(p \/ q) /\ ~(p /\ q) /codeIn other words, (p orQuestion 1 (15 marks) In digital logic, XOR is a logic operator that has the below truth table A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0 Given the following functions F= NOT(A XOR B) XOR NOT(AB), G= (AB) 1 Fill in the below truth tables of the two functions 2 Write the final logic expression of each function and conclude whether these two logic functions equivalent to each otherSome students tend to conflate "p holds knowledge sufficient to deduce q" to mean "p == q", and are surprised and indignant that the truth assignment F T in the IMPLY gate is True p → q does not mean p == q or q == p In the truth table for p → q, the result reflects the existence of a serial link between p and q

The Boolean Expression For The Output F Of The Multiplexer Shown Below Is Gate 10 Youtube

Exclusive Or Wikipedia

Truth table p xor q xor r xor s Extended Keyboard;XOR Gate Symbol, Truth table & Circuit October 12, 18 October 11, 18 by Electricalvoice A XOR gate is a gate that gives a true (1 or HIGH) output when the number of true inputs is oddTruth Table Generator This tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats For example, the propositional formula p ∧ q → ¬r could be written as p /\ q > ~r, as p and q => not r, or as p && q > !r

Proof And Problem Solving Truth Table Example 01 Youtube

Truth Table Generator Pypi

S2 1

Truth Table Widget

From Chapter 4 Formal Specification Using Z David Lightfoot Ppt Video Online Download

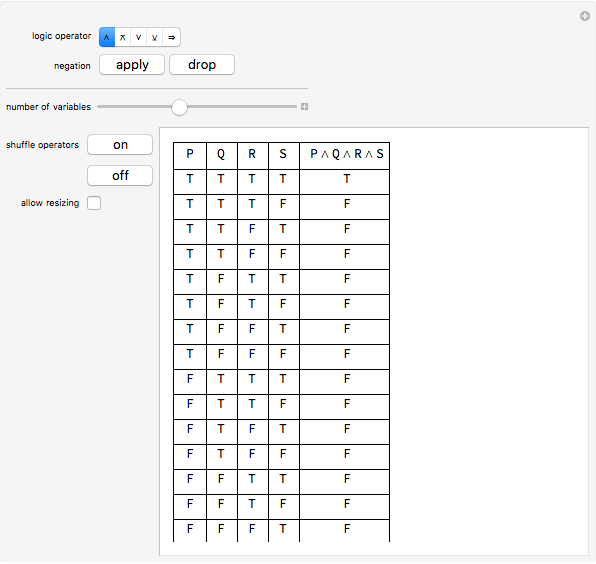
Truth Tables Wolfram Demonstrations Project

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Exclusive Or Gate Xor Gate

S2 1

Switches Gates And Circuits

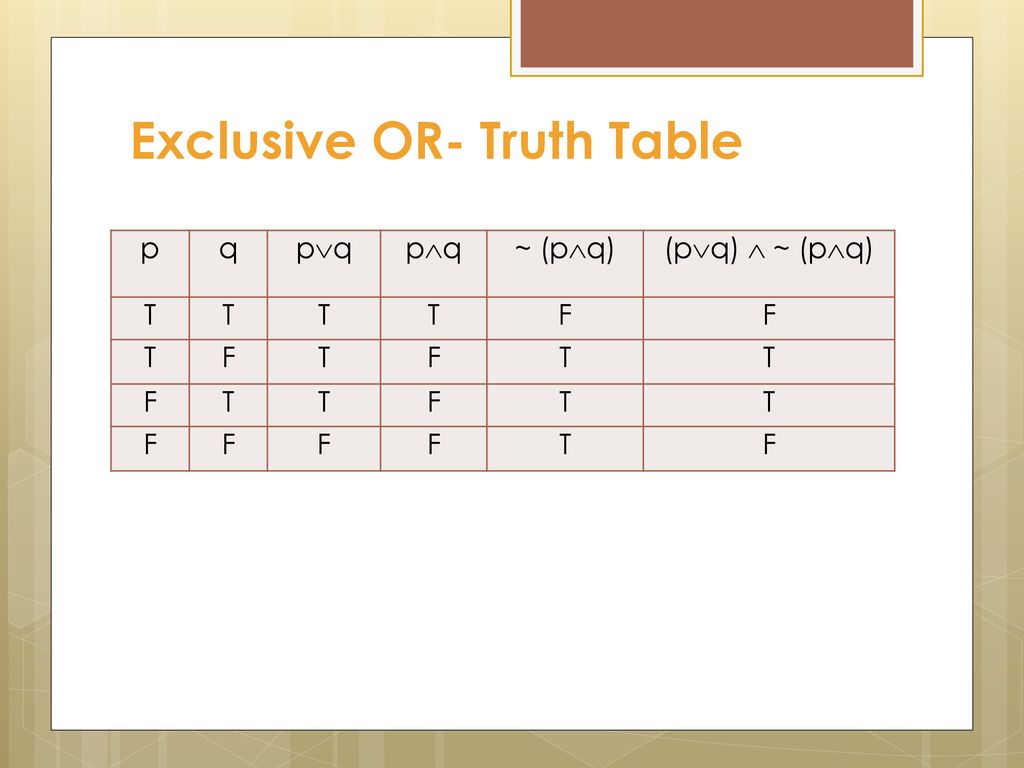
Discrete Mathematics Lecture Ppt Download

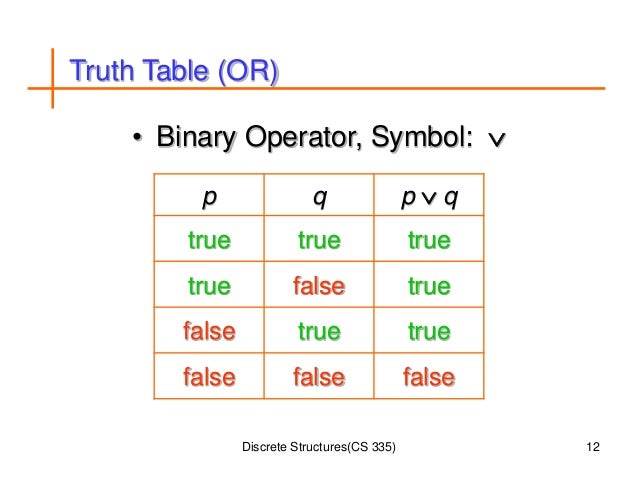
Discrete Structures Lecture 2

Applied Propositional Logic Theory Simulation Code And Digital Circuit Design Mathematical Science Technologies

Arxiv Org Pdf 1412 2287

Solved Section 1 1 1 6 Points Fill In The Following Tr Chegg Com

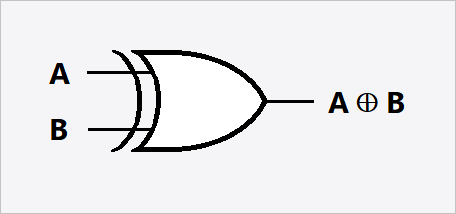
Logic Gates

Switches Gates And Circuits

Digital Logic Number Representation Geeksforgeeks

Solved M P Q P Q Xor R Chegg Com

2

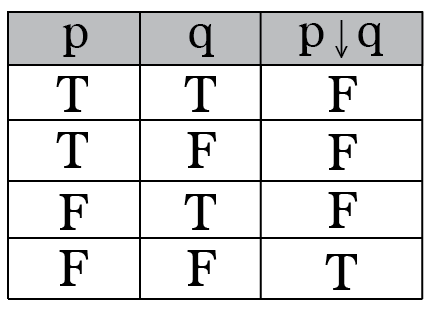
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium

Gate Cse 14 Set 3 Question 55 Gate Overflow

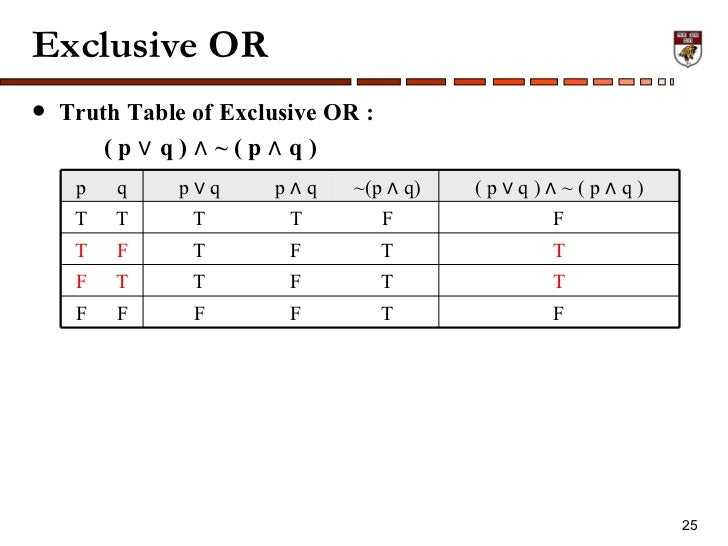
Ch1 Sets And Logic 1

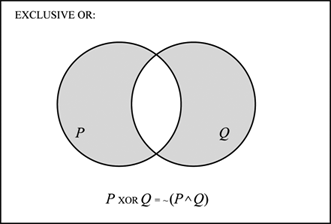
Definition Of Exclusive Or Chegg Com

S2 1

Half Truth Tables And Abnormal Forms

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

2

2 Circuits And Truth Tables Sireum Logika

Gate Solved Problems 02 08 Logic Gates Digital Electronics Youtube

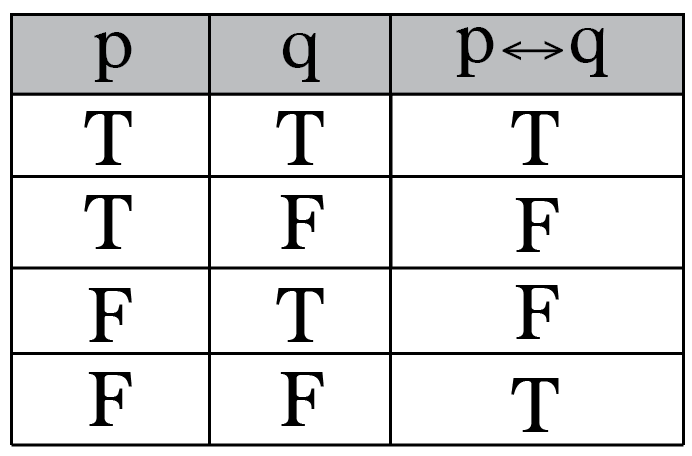
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium

S2 1

S2 1

Gate Cse 14 Set 3 Question 55 Gate Overflow

Ppt Cs 103 Discrete Structures Lecture 01 Introduction Logic And Proofs 1 Powerpoint Presentation Id

Proof And Problem Solving Truth Table Example 02 Youtube

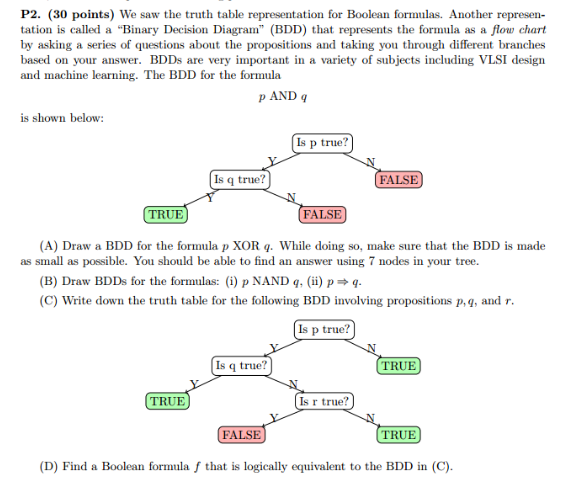
Solved We Saw The Truth Table Representation For Boolean Chegg Com

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

Discrete Mathematics Math 6a Instructor M Welling Ppt Download

2 Circuits And Truth Tables Sireum Logika

Solved Problem 6 Define The Symmetric Difference D Of Tw Chegg Com

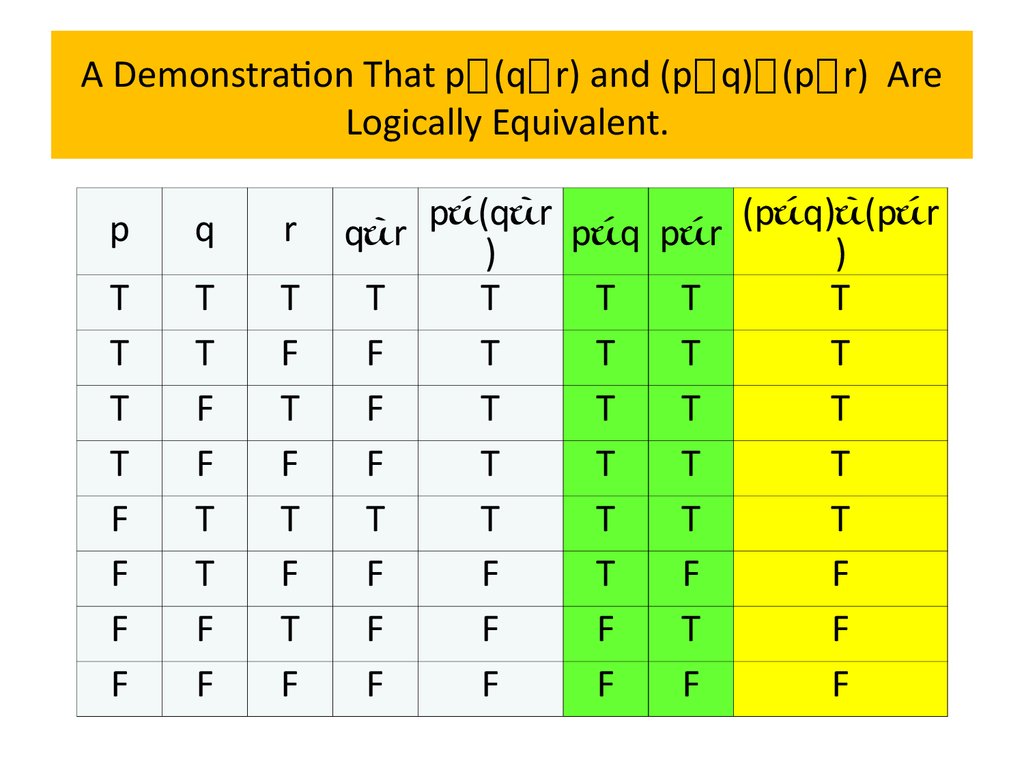
Propositional Logic Online Presentation

S2 1

Q Tbn And9gcsad2ajrh Ygvaffcqfhya3oszfu5vsobnf86xqcka Usqp Cau

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange

The Boolean Expression For The Output F Of The Multiplexer Shown Below Is Gate 10 Youtube

Solved Question 1 Mathematical Logic A Complete A Logi Chegg Com

1

Q Tbn And9gctcyhof4gcdocwu6jlnli24t1p6nwxuwa4jtsdzykcgslzibwsm Usqp Cau

Ppt Boolean Logic Truth Tables Powerpoint Presentation Free Download Id

Is Xor A Combination Of And And Not Operators Mathematics Stack Exchange

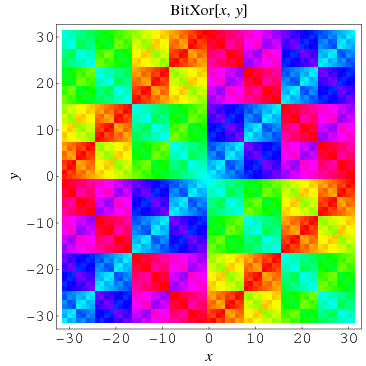
Xor From Wolfram Mathworld

离散数学之逻辑 Jason S Blog

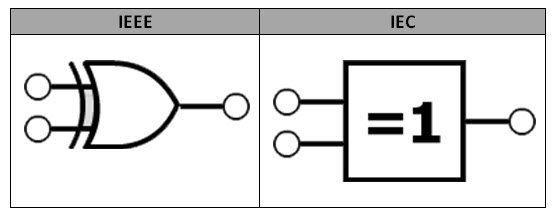
Exclusive Or Gate Xor Gate

Pts Pqr Are Boolean Variables Fill In The Following Truth Table With 0s And 1s Course Hero

Solved Construct A Truth Table For Each Of The Given Prop Chegg Com

Discrete Mathematics Logic Of Compound Statements Ppt Download

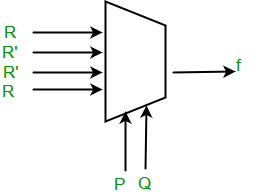
Gate Gate Cs 10 Question 65 Geeksforgeeks

Boolean Algebra Truth Table Tutorial Xor Nor And Logic Symbols Explained

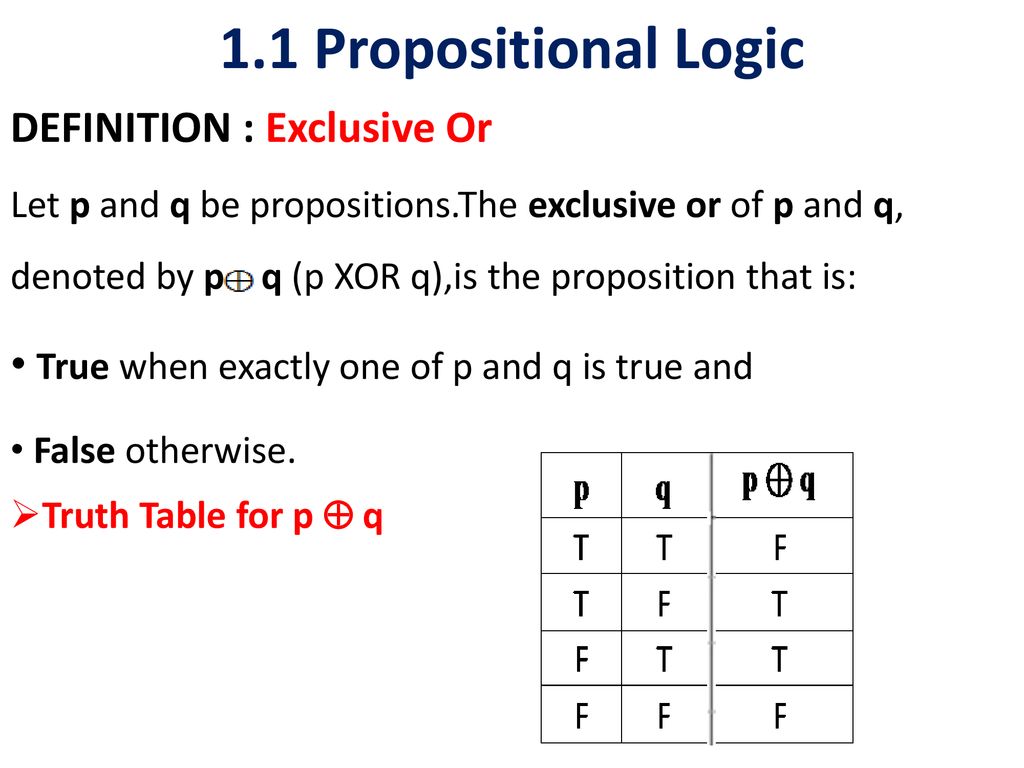
Cs 103 Discrete Structures Ppt Download

Truth Table For P Xor Q Youtube

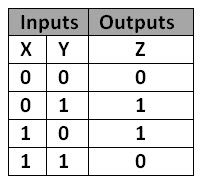
Exclusive Or Gate Xor Gate

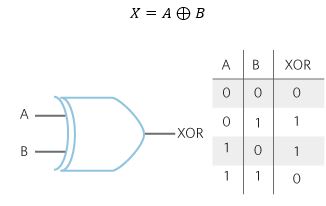
Glossary Definition For Xor Gate

2

Xor Gate or Gate Truth Table Symbol Boolean Expression Electrical4u

Mmw Truth Table Docx Dela Cruz Hannah Jane D R Bsba 1a Truth Table A Truth Table Is A Mathematical Table Used In Logic U14specifically In Connection Course Hero

Exclusive Or Wikipedia

Solved Construct A Truth Table For Each Of The Given Prop Chegg Com

Discrete Mathematics For Dummies Page 3

Here

Exclusive Or Wikipedia

Exclusive Or Wikipedia

Logic Gates Practice Problems

An Introduction To Logic Ppt Download

Incoming Term: p xor q xor r truth table,